논문을 읽기전 본 논문에서 나오는 단어 5개를 먼저 정리하려고 한다.
|
개념
|
설명
|
|
Margin
|
결정 경계와 가장 가까운 데이터 포인트 간의 거리. 넓을수록 일반화가 잘됨
|
|
Support Vector
|
결정 경계를 만드는 데 영향을 주는 중요한 포인트들
|
|
Hyperplane
|
데이터를 나누는 결정 경계. n차원 공간에서의 "직선" 또는 "면"
|
|
Feature Space
|
데이터를 고차원으로 변환한 공간. SVM은 이 공간에서 선형 분리를 시도함
|
|
Hypothesis Space
|
모델이 선택할 수 있는 함수(경계선)들의 공간
|
Introduction
- SVM(Support Vector Machine)은 데이터를 분류하거나 예측하는데 사용되는 지도학습 모델이다.
- 1992년 COLT 학회에서 Vapnik 이 처음 소개
- 일반화 성능이 뛰어나고 overfitting을 잘 피한다.
왜 SVM은 과적합을 잘 피한다고 소개하고있을까?
- SVM은 SRM(Structural Risk Minimization)이라는 원리를 따르는데, 이는 모델의 복잡도까지 고려해서, 새로운 데이터에도 잘 맞는 모델을 선택하려는 전략을 취한다.
- 반면 일반적인 신경망은 ERM(Empirical Risk Minimization) 기반인데, 이는 훈련 데이터에만 잘 맞는 모델이 될 위험이 있다고 한다.
본 논문에서는 SVM는 손글씨 인식, 얼굴 분석, 텍스트 분류와 같은 여러분야에서 사용하고, 단순 픽셀 데이터를 넣어도, 정교한 신경망 수준의 성능을 보여주고 있다고 말하며 논문을 시작하였다.
Statistical Learning Theory
통계적 학습 이론이란?
- 지식을 얻고, 예측하고, 데이터의 기반으로 결정하는 문제를 이론적으로 다루는 프레임워크이다.
지도학습의 수학적 목표
지도학습의 수학적 목표는 훈련 데이터를 잘 맞추는것이 아니라 새로운 데이터에 대해서도 잘 작동하는 함수를 찾는것이라고 말한다.

Learning and Generalization
머신러닝의 초창기 목표는 훈련 데이터에 정확히 맞는 함수(가설)을 찾는데 집중하였다.
이 말은 정답 데이터를 잘 외우는 모델을 만드는 목적이였다는 것이다.
하지만 훈련 데이터에만 너무 잘 맞으면, 새로운 데이터에서는 성능이 떨어질 수 있다.
그래서 일반화 Genralization이라는 개념이 도입되는데,
- 일반화가 잘되는 모델 = 실력자
- 일반화가 잘 안되는 모델 = 그냥 훈련 데이터를 외운 모델
일반화란 훈련에 사용하지 않는 새로운 데이터에 대해서도 잘 예측하는 능력을 말한다.

SVM이 일반화를 잘하는 이유는 복잡도와 학습 정확도 사이의 균형을 고려하였다.
쉽게 말하면, 적당히 배우고 덜 복잡하게를 추구하는 모델인 것이다.
반면 신경망은 너무 복잡해서 종종 과도하게 일반화 (over-generalization)하거나 overfitting할 수 있다.
Introduction to SVM : Why SVM?
본 논문에서 제시하는 Neural Networks는 현재의 딥러닝 모델이 아닌 1990년대 기준의 MLP 같은 비교적 단순한 구조의 신경망을 의미한다는것을 알고 읽으면 좋을것 같다.

이때의 신경망은 한계가 존재하였다.
=> MLP는 지도/비지도 학습에서 꽤 괜찮은 성능을 보였다.
=> 연속적인 비선형 함수도 잘 근사하고, 다양한 입력/출력 구조도 다룰 수 있었다.
하지만, 문제가 있었는데
- Local minima: 학습 도중 최적이 아닌 지점에 빠질 수 있음
- 구조 설계 어려움 : 몇 개의 뉴런/ 레이어가 필요한지 명확히 알기 어려움
- 유일한 해 보장 X : 학습이 수렴하더라도 항상 같은 결과가 아님
- 복잡성 증가 : 구조가 복잡해질수록 과적합 위험 증가

위 사진을 보면 두개의 데이터를 경계선(초평면)은 여러 개 존재할 수 있다.
하지만 여러개의 선들중 일부는 한쪽 클래스에 너무 가까운 선도 존재할 것이다.
그래서 SVM은 최대 마진을 갖는 경계선을 찾는 것이다.

Margin(마진)의 뜻은 경계선과 각 클래스 데이터 사이의 거리를 의미하며, Maximum Margin: 두 클래스 사이에서 가장 넓은 여유 간격을 갖는 경계선 즉, 두 클래스 사이의 거리가 같은 경계선을 찾으려고 할것이다.
마진이 넓으면 좋은점은?
- 경계선이 안정적이고,
- 경계에 약간의 오차가 있어도 오류가 잘 발생하지 않으며
- 경험적으로 일반화 성능도 좋다
라고 본 논문에서 이야기 하고 있다.
논문에 마진을 구하는 수식이 있는데,

x: 데이터 포인트 / w: 초평면의 가중치 벡터 / b: 바이어스
분자는 초평면으로부터의 거리를 의미하고, 분모는 가중치 벡터의 길이를 계산하여 나누게 된다.
SVM이 원하는 건 좋은 경계선이다
앞에서도 계속 언급하고 있지만, SVM의 목표는 단순히 데이터를 classfication이 아닌 두 클래스와의 충분한 margin을 둔 '최적의 경계선'을 찾고있는것 이다.
이때의 경계선을 초평면이라고 하는데, 이 초평면은 아래의 수식으로 정의된다.

- w: 선의 방향을 나타내는 벡터
- x: 데이터 포인트
- b: 선의 위치 조정(y절편 느낌)
이 선을 기준으로
- wx+b > 0 : 선의 위쪽
- wx+b < 0 : 선의 아래쪽
이제부터 수식이 많이 나오는데 잘 따라오길 ..
이 데이터를 제대로 분류했는지 확인하는 방법이다
모든 훈련 데이터는 (입력 xi , 정답 레이블 yi) 형태이다
예를 들어서
X1 = [2,3] , Y1 = +1
X2 = [1,-4] , Y2 = -1
일때 , 우리는 이 초평면이 두 개의 클래스에 대해 1이상 떨어지게끔 설계를 하려고 한다.

=> 케이스 1 Y1 = +1 (양 클래스)의 경우 해당 데이터가 초평면의 오른쪽에 있어야 하고,
=> 케이스 2 Y2 = -1 (음 클래스)의 경우 해당 데이터가 초평면의 왼쪽에 있어야 한다

이것이 전체 마진을 의미하는데, 마진이 커지기 위해서는
이것이 최소값이 되어야 한다.
이는 norm을 말하는데 => 벡터의 '길이' 또는 '크기'를 말한다.

을 구하려고 할 것 이다.
이때 논문에서 라그랑지안을 도입하려고 하는데, 마진을 최대화 하면서 모든 데이터가 잘 분리되게 하는 제약 조건이 있는 최적화 문제이다. 마진을 키우면서, 조건을 만족하는 w,b를 구하기 위해서이다.

이런 수식이 주어지는데, 앞부분은 우리가 최소화 하려는 마진 크기이고, 뒷부분은 조건을 맞추기 위한 식이다.
이 식을 풀면

이렇게 정의가 된다고 한다.
분류 함수
함수에 새로운 입력 데이터 x가 들어왔을 때 어느쪽 클래스인지 분류하려면?

|
구성
|
의미
|
|
αi
|
중요도 (support vector인지 여부)
|
|
yi
|
정답 레이블 (+1 또는 −1)
|
|
xi
|
훈련 데이터 중 support vector
|
|
xi⋅x
|
현재 입력 데이터와 비교되는 벡터 간 내적
|
|
b
|
경계선 조정값
|
이때 F(x) > 0 -> 클래스 +1 이라고 분류, F(x) < 0 -> 클래스 -1이라고 분류한다.
SVM Representation

Soft Margin SVM
이 식에서 앞은 모델의 복잡도를 의미하고 뒤에는 오차를 의미하는데
- 모델 복잡도는 작게, 오차는 덜 생기게 유도하는 식이다.
- 마진을 조금은 어겨도 되지만 (Soft) , 오차를 최소화하도록 제어한다.

Dual Formulation
- 커널 K 등장 -> 비선형 분리를 위한 단계
- 계산 효율성과 뒤에나오는 커널 트릭을 위해 Dual 로 변환하였다고 한다.
Soft Margin Classifier
슬랙 변수?
슬랙 변수는 '마진을 어긴 정도' 를 수치화한 값이다.
도입 된 이유는
1. 실제 세계는 데이터를 정확하게 나눌수 있는 경우는 거의 없고,
2. 아예 잘 못분류 되는 경우가 있어서
이것을 수학적으로 허용을 해주려고 변수를 넣은 것이다.
사실 이 세계에 존재하는 데이터들은 노이즈와 이상치도 있기 때문에 정확히 구분하기는 어렵다. 이때 이상치에 맞춰서 선을 구불구불하게 그릴 수 있는데, 이것은 너무 비효율적이라고 언급한다.
그래서 위와 같은 방법을 사용해 몇개의 데이터를 그냥 무시하는 방법을 채택한 것이다.
그런데, 슬랙이 너무 크다면 모든 데이터를 아무렇게나 나누는 선도 허용될 수 있으므로, 슬랙이 클수록 벌점이 주는 라그랑지안 항을 추가하여
-> 마진을 크게 유지하며, 슬랙은 최소화 되도록 조절한다.
Kernal Trick
커널 트릭은 아래와 같은 그림의 경우를 해결하기 위함이다.


이렇게 데이터가 선형으로는 분리가 안되는 경우를 고차원으로 바꿔 분리가 되도록 바꾸는 것을 커널 트릭이라고 한다. 근데 주의할 점은 진짜 고차원으로 공간 매핑을 하는것이 아닌, 커널 함수의 값을 넣어 내적값을 가지고 가는 것이다.
근데 의문이 들것이다. 내적값으로 어떻게 클래스를 나눌 수 있는것인지?
내적이란 얼마나 같은 방향인지를 숫자로 말해주는 연산이다.
아 그러면 두 데이터 간의 유사도를 구할 수 있는 식이구나! 라고 생각하면 될 것 같다.
요약하자면, 커널 트릭을 통해 고차원 내적값을 알면, 데이터가 어느 클래스에 더 가까운지 판단하여, 이것을 기준으로 데이터를 구별하는것이다!
Kernal Trick: Dual Problem
커널을 쓰려면 고차원으로 데이터를 보내야 하는데, 이 방식은 w를 집접 다루기 때문에 계산이 어려워진다고 한다.
그래서 w를 직접 계산하지 말고, 모든 계산을 '내적'으로 바꾸려고 하는것이다.

아까 썼던 수식을 가져와서 w를 벡터간 내적으로 표현한다.
Kernal Functions
커널 함수를 통해 고차원으로 보내 내적을 해야 했던 것을 그냥 내적한 것처럼 계산해주는 함수를 말하는데, 본 논문에서 4가지 커널 함수들을 소개하고 있다.
|
번호
|
커널 이름
|
수식
|
특징 / 설명
|
주요 하이퍼파라미터
|
|
1
|
선형 커널 (Linear)
|
K(x,x′)=x⋅x
|
가장 단순한 커널. 고차원 변환 없이 사용.
|
없음
|
|
2
|
다항 커널 (Polynomial)
|
K(x,x′)=(x⋅x′)^d
또는
K(x,x′)=((x⋅x′)+1)^d
|
차수 dd
d에 따라 복잡한 비선형 경계 가능.
|
차수 d
|
|
3
|
가우시안 RBF 커널
(Gaussian Radial Basis Function)
|
아래 그림 참고
|
가장 많이 사용됨. 거리 기반 유사도 측정. 부드러운 경계 형성.
|
σ (폭)
|
|
4
|
지수형 RBF 커널
(Exponential RBF)
|
아래 그림 참고
|
가우시안보다 급격한 변화. 불연속 허용.
|
σ
|
|
5
|
MLP 커널
(Multi-Layer Perceptron)
|
K(x,x′)=tanh(ρ⋅x⋅x′+θ)
|
신경망(퍼셉트론) 유사. 비선형 활성화 효과.
|
ρ,θ
|
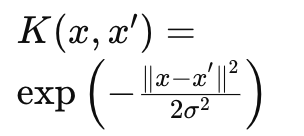
가우시안 RBF 커널

지수형 RBF 커널
이렇게 설명하고 있다.
Controlling Complexity in SVM: Trade-offs
SVM은 어떤 데이터든 잘 분류할 수 있는 강력한 모델이지만, 복잡한 모델일수록 overfitting이 일어날 수 있어서 복잡도를 잘 조절 해야한다고 한다.

training error 와 confidence term 의 합이 최소가 되는 지점을 골라야 한다!
conclusion
- SVM은 통계적 학습 이론에 기반한 모델이다.
- 미래 데이터를 예측하기 위한 학습에 이용할 수 있다.
- 입력 데이터를 커널 함수를 통해 고차원 공간에 있는것처럼 계산하여 분류한다
- SVM에는 최적의 해가 존재한다.
작성자의 한마디
수식이 너무 많아 어렵네요.. 저도 이해를 잘 하지 못했는데 혹시라도 틀린 설명이 있다면 알려주세요..



