Introduction
데이터 마이닝이란?
- 데이터 마이닝은 다양한 관정에서 데이터를 분석해 유용한 정보를 추출하는 기술
- 주로 사용되는 분야: 인공지능, 머신러닝, 통계학, 데이터베이스
데이터 마이닝의 주요 작업
- anomaly detection (이상 탐지)
- association rule learning (연관 규칙 학습)
- clustering (군집화)
- classfication (분류)
- regression (회귀)
- summarization (요약)
- sequential pattern mining (순차 패턴 마이닝)
=> 현재 본 논문은 classification에 초점을 맞춰서 설명함
Classification ?
- label이 있는 학습 데이터를 통해 모델(분류기)를 학습시킴 -> 이후 새로운 데이터의 label을 예측하게 한다
- 수식 적으로는 아래와 같다.
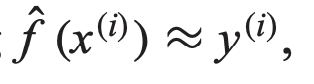
입력 x로 부터 정답 y를 예측
- 예측 변수(X)는 범주형이 될 수 있고, 연속형도 가능하다
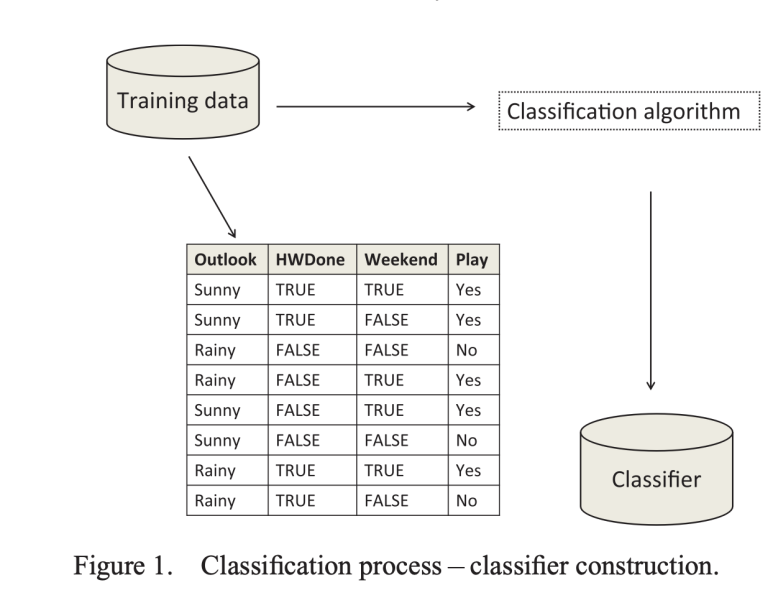
논문의 나온 사진을 보면, feature (본 논문에서는 attribute라고 표현함)가 총 4개 , Data instance가 8개임을 확인 할 수 있다
이렇게 주어진 데이터셋을 학습 후 레이블이 없는 데이터를 결정하는 것이 목표다.
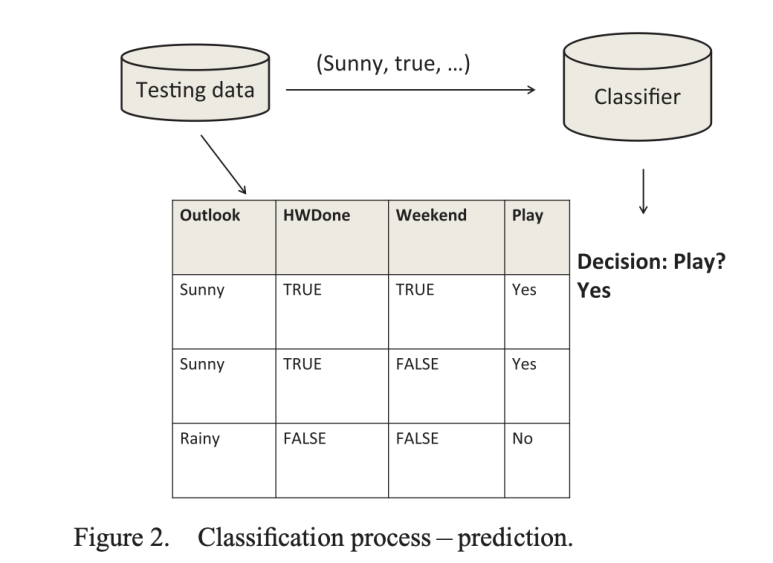
single classifier 는 성능에 제한이 존재하므로, 본 논문에서는 앙상블 학습(ensemble learning)의 Random Forest(RF)의 역사적 발전, 기술적 상세 설명, 확장 기법, 응용 사례, 미래 발전 방향에 관해서 다룰려고 한다.
BackGround on Ensemble Classification
앙상블 분류란?
앙상블 분류(ensemble classificaion)는 여러 개의 분류기를 조합하여 정확도를 높이는 방법을 말한다.
앞서 논문에서 이야기 했듯이, 단일 분류기는 한계가 존재하므로, 여러 모델을 함께 사용함으로써 정확한 예측이 가능하도록 만들기 위함이다.
본 논문에서는 Voting Scheme를 3가지를 소개하고 있다.
- Majority Voting(다수결)
- 가장 많이 선택된 클래스가 최종 결과가 된다.
- 모든 분류기가 동등한 표를 가진다는 특징이 있다.
- Veto Voting (비토 방식)
- 특정 분류기가 다른 분류기들의 예측을 거부(veto) 가능하다.
예를 들어, 5개의 분류기가 있을 때
|
분류기
|
예측 결과
|
|
A
|
고양이
|
|
B
|
고양이
|
|
C
|
고양이
|
|
D
|
고양이
|
|
E
|
강아지
|
이렇게 예측했다고 보자, E 분류기에서 혼자 강아지라고 예측을 했는데, Majority 투표 방식은 4:1 이므로 고양이라고 결정을 내리겠지만 Veto Voting에서는 1개라도 반대 의견이 존재하다면 최종 결정을 무효 or 보류 한다는 것이다.
- Trust-Based Veto Voting (신뢰 기반 비토)
- 신뢰도가 높은 분류기만 비토가 가능하다
- 각 분류기 신뢰도를 기반으로 결정한다.
아까 Veto Voting에서 모든 분류기가 Veto가 가능했다면 신뢰 점수가 높은 분류기만 Veto 권한을 보유하게 된다.
|
분류기
|
예측
|
Trust 점수 (0~1)
|
|
A
|
고양이
|
0.95 ✅
|
|
B
|
고양이
|
0.90 ✅
|
|
C
|
고양이
|
0.85 ✅
|
|
D
|
고양이
|
0.50 ❌
|
|
E
|
강아지
|
0.30 ❌
|
위에 있었던 분류기에 신뢰도 점수를 부여하여 보면 E는 강아지라고 예측했지만 신뢰점수가 낮아 Veto가 불가능하게 된다. 그래서 위의 경우와 다르게 고양이로 결정을 내리게된다.
좋은 앙상블의 조건
- 정확도(accuracy): 무작위 추정보다 잘 맞춰야 한다
- 다양성(diversity): 서로 다른 오류를 범해야 함 -> 다양할수록 예측이 강해진다
서로 다른 오류를 범해야한다라는 말이 조금 어려울 수 있지만, 시험 문제를 풀때 여러명이 함께 풀면 누구는 틀릴수도, 누구는 맞출 수 있기 때문이라고 이해하면 좋을 것 같다. 만약 나와 같은 사람이 3명이 존재하는것과 서로다른 사람 3명이 존재하면 더 맞출 확률이 올라갈수있다는 논리인 것이다.
대표적인 앙상블 기법
본 논문에서 총 3가지의 앙상블 기법을 소개 하고 있다.
표로 정리하면
|
기법
|
개념
|
장점
|
단점
|
|
Boosting
|
이전 분류기가 틀린 데이터를 다음 분류기가 학습
|
높은 정확도
|
노이즈에 약하고 과적합 위험
|
|
Bagging
|
여러 샘플을 무작위로 뽑아 병렬 학습 (예: Random Forest)
|
과적합에 강하고 안정적
|
Boosting보다 정확도 낮을 수 있음
|
|
Stacking
|
여러 모델의 예측 결과를 또 다른 모델이 통합
|
성능 향상 기대 큼
|
복잡도 높고 학습 오래 걸림
|
이렇게 정리를 하였고, Dietterich가 2000년에 수행한 실험에서는
데이터셋에 noise가 없다면 Boosting이 좋은 성능을 보였지만, noise가 많아질 수록 Boosting의 성능이 내려갔다고 한다. Bagging은 노이즈가 많아도 성능이 유지가 되었다고 설명하고 있다.
그러면 앙상블을 선택할때는 데이터가 노이즈가 많은지의 여부와 모델의 특성을 고려하여 선택해야함을 시사한다.
Earlier Developments to Random Forests
전통적인 결정 트리는 학습 데이터에 대해 질문-기반 분할을 통해 데이터를 분류한다.
이때 두가지의 한계점이 존재하는데,
- 복잡성 제한
- 트리를 깊에 키울수록 훈련 데이터에 과하게 적합 (overfitting)
- 반대로 트리를 작게 만들자니, 복잡한 패턴을 포착하지 못함 (underfitting)
-> 복잡도를 마음대로 키울 수 없다는 근본적인 한계가 존재한다고 한다.
2. 고정 길이 벡터 기반 학습의 비현실성
- 전통적인 트리는 일반적으로 입력을 고정된 길이의 특징 벡터로 표현한다고 하지만 이미지나
비정형 데이터의 경우, feature의 개수가 너무 많이 존재한다.
그래서 본 논문에서 3가지 아이디어를 소개하고 있다.
1. Oblique Decision Tree (경사 분할 트리) - Ho (1995)
전통적인 결정 트리의 경우
if 키 <= 170 : -> YES : 그룹 A -> NO : 그룹 B이렇게 구분 하였는데, 현실의 데이터들은 이렇게 하나의 feature로 나눌수가 없으므로, 키와 몸무게 등 여러가지 특성을 고려해야한다. 그래서 여러 특성을 조합하여 그룹을 나누기 위한 방법을 고안한 것이다.
2. Randomized node optimization (무작위 노드 최적화) - Amit & German (1997)
모든 feature을 고려해서 최적의 분할을 찾는 것은 현실적으로 불가능하므로,
그 중 몇개만 무작위로 골라서 분할 기준을 찾는 방법 한 트리에서 각 노드마다 선택되는 특성이 달라진다.
3. Random Subspace (무작위 부분공간) - Ho (1995)
특성이 너무 많으면 아예 트리마다 보는 특성 자체를 다르게 해보려는 방법이다.
- 각 트리는 전체 데이터에서 무작위로 고른 몇 개의 특성을 사용해서 학습하려고 한다.
- 그러면 각각 트리마다 다른 관점을 가진 트리들이 생성된다.
==> 이렇되면 서로 다른게 보는 모델을 모으면 하나의 관점이 놓진 부분을 다른 트리가 채워줄 수 있게 된다.
Random Forest
랜덤 포레스트란?
여러 개의 결정 트리를 무작위로 생성하여, 이들의 예측을 다수결로 통합하는 구조를 가진다.
- Bagging
- 무작위 특성 선택
이 두개의 기법의 결합이다.
작동 원리
1. 트리 구성: Bagging 사용
- 훈련 데이터에서 복원 추출로 여러 샘플을 만든다.
- 각 샘플을 가지고 트리를 하나씩 학습한다
- 전체 훈련 데이터의 64%는 In-Bag 으로 사용되고 36%는 out-of-Bag으로 남긴다.
2. 노드 분할: 특성 무작위 선택
- 각 노드에서 데이터를 분할할 때는 전체 특성이 아닌 무작위로 선택된 부분집합만을 고려해야한다.
- 이중 Gini index가 가장 낮아지는 특성을 선택하여 분할한다.
- 일반적인 결정 트리는 모든 특성을 비교해서 가장 좋은 기준을 찾지만, RF는 일부 특성만을 무작위로 뽑아서 좋은 기준을 찾는 방법을 말한다.
- 이 부분이 overfitting을 방지하는 방법이라고 한다.
3. 예측: 다수결 투표
- 학습이 끝나면, 새로운 샘플에 대해 모든 트리의 예측을 모아 다수결로 결정한다.
GIni Index 에 관해 조금 더 설명하자면
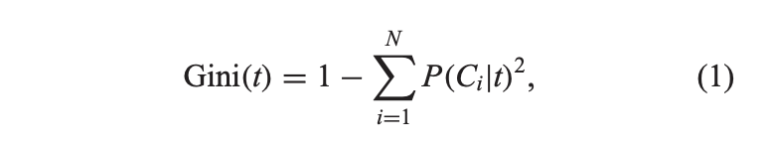
일단 수식은 이렇다. t는 현재 노드 , 확률은 노드 t에서 클래스 Ci의 비율을 의미한다.
예시를 들어서 설명을 해보려고 한다.
- 순수한 노드의 경우 (Gini = 0)
- 데이터 10개중 10개가 전부 class 하나로 분류됨
- P(A|t) = 1 -> Gini = 1 - (1)2 = 0 이다.
2. 혼합된 노드의 경우 (Gini = 0.5)
- class A : 5개 , class B : 5개
- P(A|t) = 0.5, P(B|t) = 0.5 -> Gini = 1 - (0.52 + 0.52 ) = 1 - 0.5 = 0.5
데이터를 둘로 나눌 때 지니기수가 낮아지는 기준을 선택한다
과적합을 막는 방법
본 논문에서는 RF가 overfitting을 제한한다고 언급하고 있는데
이유는
- 트리 간 낮은 상간관계 => 서로 다른 관점을 가진 트리들이 만들어지고
- 트리 개별 성능 => 각 트리의 예측력이 충분히 높아서
결과적으로 전체 앙상블의 error rate가 낮아진다고 한다.
한마디로 정리하면, 트리끼리 비슷하거나 트리가 약하면 앙상블이 쓸모 없어진다는 이야기다.
RF extention
|
연구자
|
제안 기법
|
주요 내용 및 목적
|
|
Latinne et al. (2001)
|
McNemar 검정 기반 선택
|
과도한 트리 수 제한
정확도 손실 없이 적은 트리만 사용
|
|
Robnik-Šikonja (2004)
|
다중 특성 평가 + 가중치 투표
|
트리 간 상관성 감소
일반 다수결 대신 가중치 기반 투표
|
|
Tsymbal et al. (2006)
|
동적 통합(Dynamic Integration)
|
고정 다수결 대신 DS, DV, DVS 기반 동적 통합 투표
|
|
Amaratunga et al. (2008)
|
가중치 기반 랜덤 샘플링
|
특성이 많고 중요한 특성 수가 적을 때 성능 하락 개선
가중치 기반 특성 선택
|
|
Saffari et al. (2009)
|
온라인 RF 알고리즘
|
오프라인 RF 한계 극복
실시간 학습이 가능한 RF 구조 제안
|
|
Bader-El-Den & Gaber (2012)
|
유전 알고리즘 (GA) 적용
|
유전 알고리즘으로 RF 성능 향상
|
|
Xu et al. (n.d.)
|
하이브리드 RF
|
고차원 데이터에 특화된 하이브리드 RF 제안
전통 RF보다 뛰어난 성능
|
RF application
|
연구자
|
분야
|
목적
|
활용 요약
|
|
Cutler et al. (2007)
|
생태학
|
종(species) 분류
|
다양한 분류 기법과 비교 → RF가 가장 우수한 정확도 보임
|
|
Klassen et al. (2008)
|
의학
|
암 분류
|
실험을 통해 마이크로어레이 유전자 데이터 분류에 탁월한 성능 입증
|
|
Hu (2009)
|
의학
|
유방암 병리학적 완전 반응 예측
|
중요 유전자를 식별하는 데 효과적이었으며, 생물학적으로 의미 있는 특성도 파악 가능
|
|
Gao et al. (2009)
|
천문학
|
천체 객체 분류
|
다중 파장 데이터에 대해 실험, RF가 분류 정확도 높게 나타남
|
|
Flaxman et al. (2011)
|
법의학 (부검)
|
사망 원인 예측
|
새로운 CCVA(Computer-Coded Verbal Autopsy) 방식에 RF를 결합하여 예측 정확도 향상
|
|
Zaklouta et al. (2011)
|
교통계획
|
교통 표지판 분류
|
K-d 트리 + RF 조합 사용, 다양한 HOG 기술 + 거리 변환으로 43개 표지판 분류
|
|
Löw et al. (2012)
|
농업
|
작물 분류
|
RF + SVM 조합 사용, 지도 기반 불확실성까지 고려한 고정밀 작물 분류 가능
|
|
Boulesteix et al. (2012)
|
생물정보학
|
RF 기반 연구 동향 조사
|
최근 10년간의 RF 적용 사례들 종합 분석 → 바이오 분야 대표적 적용 예시 제공
|
Discussion & Summary
랜덤 포레스트는 단순히 좋은 분류기 그 이상이며, 다양한 기법과 조합을 통해 계속해서 발전하고 있다. 앞으로도 실용성과 해석력을 동시에 갖춘 강력한 모델로 활약할 것이다.
작성자의 한마디
영어 공부 열심히 하고... 힘드네요 이번논문



